Conception de cames


Dimensionnement de cames

Le dimensionnement de cames est omniprésent et fondamental dans l'industrie d'aujourd'hui. Il participe, fortement, du génie mécanique contemporain et prend une place prépondérante dans le dimensionnement mécanique. Les cames permettent de "programmer" le mouvement. Le principe est de concevoir une forme géométrique permettant d'avoir un degré de contrôle sur le mouvement; par exemple lorsque l'on veut maîtriser les temps d'ouverture et de fermeture des soupapes automobiles (principe de l'arbre à cames) pour gérer les cycles thermodynamiques dans les chambres de combustions. Et ceci n'est qu'un exemple d'utilisation des cames qui sont, au risque de nous répéter, de véritables outils de programmation du mouvement.

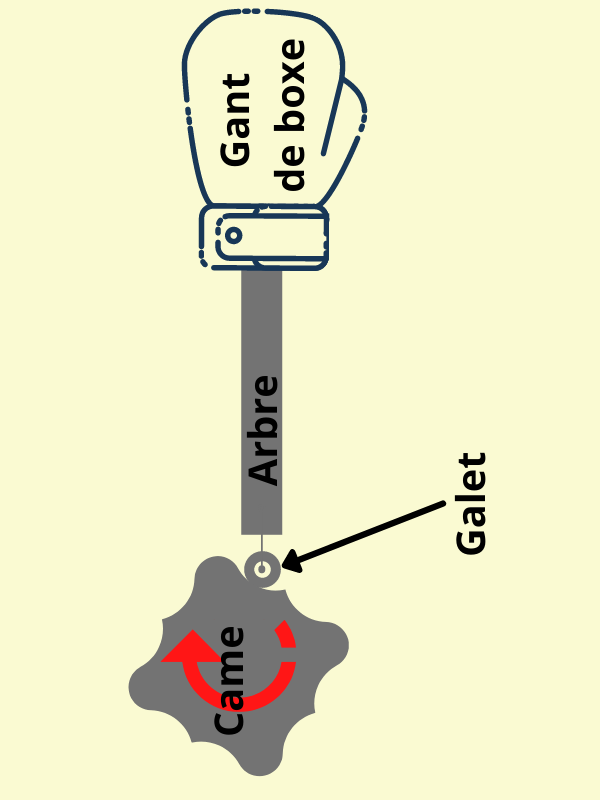
Dans notre cas, nous allons prendre un exemple à titre illustratif, comme schématisé sur l'image ci-après. En effet, dans cette dernière, nous constatons qu'une came, avec un exemple de forme donné, est en rotation et va induire, de par sa géométrie, un mouvement rectiligne alternatif de l'arbre, lui-même relié au gant de boxe. On comprend donc qu'en fonction de la course que l'on voudra donné au gant de boxe, la géométrie de la came sera différente et induire le/les mouvement(s) désiré. C'est ici ce que l'on propose d'effectué.

La course

Tout part de la course. Ici, on propose celle représentée dans le graphique juxtaposé au paragraphe. On considère un cycle de 12 secondes. On donnera une vitesse angulaire constante à la came. Toutes les deux secondes, le gant de boxe aura avancée d'une distance de 10 cm (et aura mis deux secondes pour arriver à cette position) et reviendra à sa position initiale et mettra deux secondes pour revenir à cette position (il aura donc reculé d'une distance de 10 cm). Les transitions se feront sinusoïdalement de sorte que la course "c" soit une fonction sinusoïdale dépendante du temps positif "t" : \(c(t) = 5cos(\omega t+ \pi)+5\). Pour que la course corresponde aux conditions précédemment énoncées, on déduit que la vitesse angulaire \(\omega\) vaut \(\frac{\pi}{2}\ rad.s^{-1}\). Finalement, la course se définie comme suit : \begin{equation} c(t) = 5\left(cos\left(\frac{\pi}{2} t+ \pi\right)+1\right) \end{equation} Bien entendu, il s'agit là du déplacement du gant et non de sa position. Autrement dit, le gant a une position initiale "x0" à laquelle on ajoute la course "c(t)" en fonction du temps. Ainsi, nous écrivons que la position du gant à un instant donné vaut : x(t) = x0+c(t).

Grâce à l'expression de la course, nous pouvons calculer la vitesse de déplacement, l'accélération et l'impulsion du système {gant} (ou un point fixe par rapport à un repère lié au gant) dans le repère vertical dont l'origine est confondue avec le centre de rotation de la came. Cela nous permet de connaître, entre autres, des éléments tels que la pression de contact ou la vitesse de déformation (s'il y a déformation) et donc de faire des choix de matériaux et de dimensionnement adéquats (par exemple pour le galet en contact avec la came). Nous ne traiterons pas cet aspect dans le cas présent. Le tracé de la came étant l'objectif du présent écrit.

Tracé du profil de la came

Connaissant la course, nous pouvons déduire le tracé du profil de la came. Pour ce faire, il suffit de projeter la course verticale \(c(t) \cdot \overrightarrow{x}\) dans le repère lié à la came\( \{\overrightarrow{x\prime},\overrightarrow{y\prime}\} \) en rotation, d'un angle \(\theta(t) = \omega t = \frac{\pi}{2} t\), par rapport au repère vertical (cf. illustration sur la figure de gauche). En bref, cela revient à exprimé la course dans le repère lié à la came. Voici ce que l'on obtient :


Forts de ces projections, nous pouvons tracer le profil de la came (cf. figure à droite), en précisant certains éléments : il faut connaÎtre le temps d'un cycle complet de rotation de la came. Car, en effet, il s'agit de tracer une courbe paramétrique (ici on peut choisir le temps ou l'angle de rotation* comme paramètre). La came aura fait un cycle lorsque l'angle de rotation vaudra \(2\pi\) (360°). Le temps de cycle "tcycle" est donc tel que : \begin{equation} \omega t_{cycle} = 2\pi \Leftrightarrow \frac{\pi}{2} t_{cycle} = 2\pi \Leftrightarrow t_{cycle} = 4\ s \end{equation}

La résolution de l'équation montre que le temps de cycle est de 4 secondes. On choisit donc un paramètre de t (représentatif du temps) qui variera entre 0 et 4 secondes et on calculera les angles correspondant en chacun des instants. Aussi, on considérera la came, dans un premier temps, comme étant un cercle régulier (de rayon 15 cm) dont la surface sera modifiée (creusée ou extrudée) en fonction de l'angle (dépendant du temps) durant un temps de cycle. Ainsi, nous pouvons tracer le profil de notre came en utilisant un diagramme radar (i.e. à chaque angle de rotation, on associe une distance \(\sqrt{x_p^2+y_p^2}+15\ \)correspondant à la norme, du vecteur \(x_p(t)\overrightarrow{x\prime}+y_p(t)\overrightarrow{y\prime}\), à laquelle on rajoute les 15cm du rayon du cercle "imaginaire" initial) comme sur la figure de droite. Le gant est enfin prêt à monter sur le ring !... Enfin, pas vraiment : on comprend qu'en plaçant ce dernier profil de came au contact du galet (lui-même relié à un arbre relié au gant), nous pouvons, moyennant la rotation de la came, générer le mouvement alternatif du gant de boxe. Mais encore faut-il choisir le bon galet, dimensionner l'arbre (et la façon dont il sera assemblé au galet et au gant) , élire un moteur pour faire tourner la came, choisir les bons matériaux...etc. Il y a encore beaucoup à faire mais nous savons, à présent, la méthodologie à employer pour concevoir le profil d'une came.




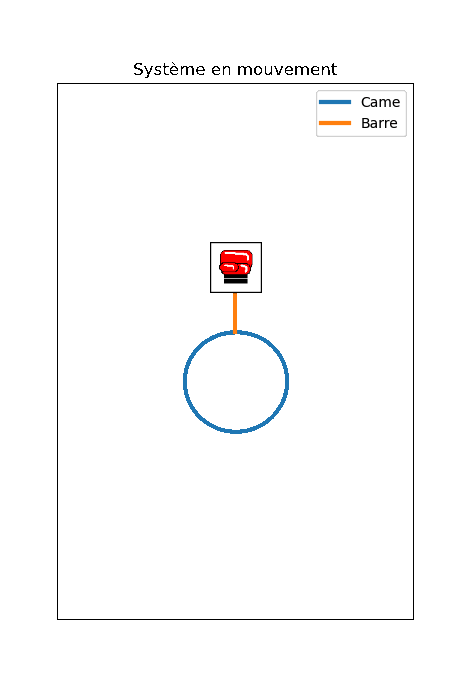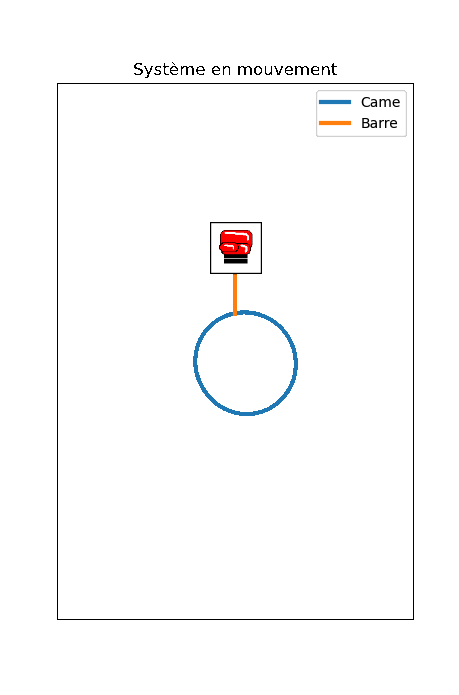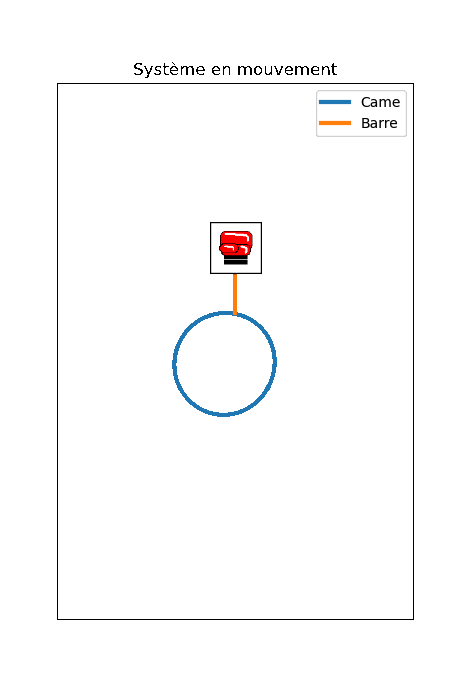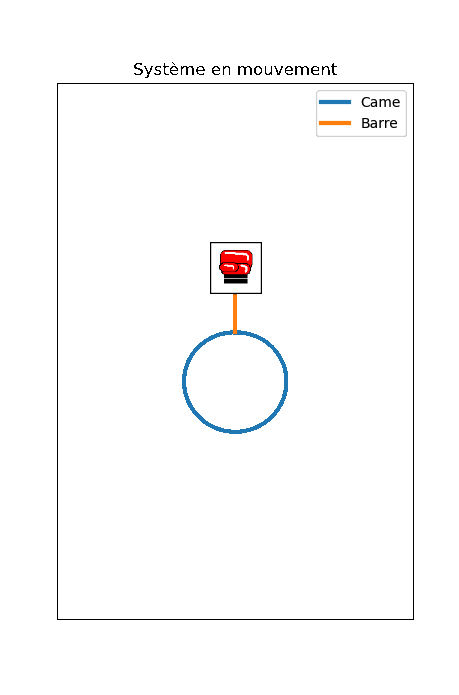
Après avoir tracé ce profil, il faut garantir que d'autres paramètres physiques (critère de non décollement, pression de hertz...) soient cohérents avec les objectifs visés. De même, il faudrait concevoir les solutions technologiques d'assemblage des composants du système. Nous n'aborderons pas ces éléments ici; nous émettons l'hypothèse que le dimensionnement est adéquat. Nous proposons en conséquence une animation à titre illustratif, afin de visualiser une utilisation possible d'une came.