Régression logistique binaire

La régression logistique, au même titre que d’autres types de régression (polynomiale, linéaire, exponentielle…), est une méthode d’apprentissage automatique permettant des usages en classification notamment. Eh oui, classification et régression ne sont pas nécessairement opposées. On utilise une méthode de régression pour classifier des données dans deux classes ou identifier une tendance (i.e. quantifier à quel point un individu appartient à une classe), et ce, en fonction d’une ou plusieurs caractéristiques. Dans le graphique juxtaposé, on observe une illustration généralisée et schématique d’une fonction logistique permettant de classifier des données selon deux modalités : la classe E et la classe F (distincte de E). Cette classification se ferait, dans le cas évoqué, sur la base d’une (et une seule) caractéristique que l’on nomme "x". D’autre part, l’expression de la fonction logistique est indiquée. On constate que plusieurs paramètres détermine une telle fonction :

Remarque: En machine learning, il est parfois question de fonction sigmoïde (fonction d’activation dans les réseaux de neurones par exemple) qui est un cas particulier de fonction logistique où A = 1, a=1 et b=0

Le contexte général d’une fonction logistique ayant été brièvement défini, nous proposons à présent un cas d’application. Nous essaierons d’opérer une régression logistique sur un jeu de données d’étude, afin de distinguer deux classes. Nous nous limiterons à une seule caractéristique afin de distinguer les deux catégories (pour mieux visualiser et comprendre le principe de fonctionnement d’une régression logistique). Enfin, nous tenterons d’établir une méthodologie d’évaluation de la performance de notre régression pour classifier les données ou identifier les tendances d’appartenance.

Brève analyse

En guise d’exemple, nous travaillerons sur un extrait du jeu de données issue de la librairie "seaborn". Le nom du dataset (dont nous extrayions les données) est "attention". Globalement, les données sont des notes de tests et un niveau d’attention (concentré ou "dissipé"") d’individus ayant passé un examen. Voici les première données de notre dataset:

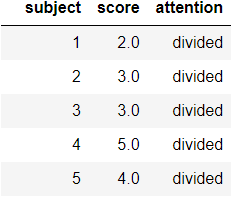
L’étude analytique de la base de données peut faire l’objet d’une activité complète. En effet, il est important de savoir les dynamiques, les relations, de même que les biais sous-jacents qui définissent le jeu de données, car il est déterminant dans la manière de traiter les données, d’implémenter les algorithmes et d’interpréter nos résultats. Dans notre cadre, il semble qu’il suffit de noter qu’il existe un certain équilibre dans le dataset. En effet, nulle modalités, ni aucun sujet examiné n’est sur représenté. Chaque modalité apparaît 30 fois et chaque individu est évalué trois fois.



Enfin, nous constaterons que le score, variable continue (et explicative de notre modèle logistique) suit une distribution que l’on peut, globalement, considérer comme normale avec une moyenne d’environ 6 et un écrat-type d’environ 1.5.




Optimisation – descente de gradient

À nouveau, L’objectif est de faire le lien entre les notes et les niveaux d’attention, par régression logistique, et d’analyser la performance du modèle ainsi conçu. Pour ce faire, on codifie les deux états possibles par 0 et 1 pour divided (distrait) et focused (concentré) respectivement; autrement dit, le paramètre A vaut 1 car il sera le maximum de la fonction logistique. On choisit de minimiser les moindres carrés(1) (i.e. trouver les paramètres a et b tels que la somme des distances verticales soit minimisée). Aussi, on notera les scores et les niveaux de concentrations répertoriés dans notre dataset de 60 éléments. Ainsi, la somme des distances entre le modèle et les points expérimentaux vaut: \begin{equation} \tiny {C(a,b) = \frac{1}{60} \sum_{i=1}^{60} \left(y_i - \frac{1}{1+e^{-a(x_i-b)}}\right)^2} \end{equation} Pour des raisons de simplifications, nous omettrons ici les calculs intermédiaires (l’objectif étant de montrer le principe de fonctionnement et les applications possibles de telles méthodes). Par conséquent, voici le gradient de la fonction fonction coût précédemment évoquée: \begin{equation} \vec{\nabla}C(a,b) = \left( \begin{array}{c} \frac{1}{60} \sum_{i=1}^{60} 2\left(\frac{1}{1+e^{-a(x_i-b)}}-y_i\right)\left(1-\frac{1}{1+e^{-a(x_i-b)}}\right)\frac{x_i-b}{1+e^{-a(x_i-b)}}\\ \frac{-1}{60} \sum_{i=1}^{60} 2\left(\frac{1}{1+e^{-a(x_i-b)}}-y_i\right)\left(1-\frac{1}{1+e^{-a(x_i-b)}}\right)\frac{a}{1+e^{-a(x_i-b)}} \end{array} \right) \end{equation} Pour rappel, il s’agit ici de minimiser la fonction coût, pour la simple raison que plus la sortie du modèle logistique est proche de la vérité terrain, plus l’erreur sera faible. Forts du gradient et de la fonction coût, nous pouvons maintenant utiliser un algorithme d’optimisation pour minimiser l’erreur quadratique moyenne. Nous proposons d’utiliser une descente de gradient à pas fixe (pratique dans ce cadre). Cette méthodologie repose sur le principe suivant: en un point quelconque, qui n’est pas l’extremum d’une fonction, puisque le gradient pointera vers le maximum/minimum de cette même fonction, nous pouvons choisir un nouveau point en suivant la direction du gradient(2), lui même plus proche de l’extremum recherché. En conséquence, en procédant de manière itérative, nous pouvons, au fur et à mesure nous rapprocher, voire trouver le point extremum de la fonction. De plus, la norme du gradient sera nulle en cette extremum, indicateur sur lequel on pourrait se baser pour savoir si l’on est plus ou moins proche d’un extremum (si la fonction est suffisamment "lisse"). Il y a bien entendu des éléments auxquels il faut faire attention comme le choix du pas d’avancement:s’il est trop faible, l’algorithme mettra du temps à fournir un résultat satisfaisant; si a contrario, il est trop élevé, il y a un risque de divergence (croissance incontrôlée du gradient). Les paramètres que nous choisissons sont les suivants:

Notons que le choix de ces paramètres peut s’avérer très déterminant dans l’obtention de résultats satisfaisants. Il existe des méthodes pour aider ces choix. Une approche plus expérimentale consiste à tester des valeurs jusqu’à trouver une combinaison adéquate. Enfin, à chaque itération \(k\) (\(k \in \mathbb{N}\)), le point (ou vecteur) suivant, de coordonnées \((a_{k+1},b_{k+1})\), est actualisé selon l’équation suivante: \begin{equation} \left[ \begin{array}{c} a_{k+1}\\ b_{k+1} \end{array} \right] = \left[ \begin{array}{c} a_{k}\\ b_{k} \end{array} \right] - pas \times \vec{\nabla}C(a_k,b_k) \end{equation}

Résultats obtenus sur tout l’échantillon

Voici les résultats que l’on obtient après avoir effectué une régression logistique sur tout l’échantillon:

La solution optimale est environ (0.85 ; 5.89). Elle est atteinte au bout de 8915 itérations. Le résidu final (norme du gradient au point résultant de l’algorithme) est de l’ordre de 10-14 donc relativement proche de zéro; la solution correspond très probablement à un minimum.

Convergence

L’analyse de la courbe d’apprentissage montre que l’algorithme converge bien vers la solution choisie. On observe aussi qu’avant d’atteindre cette solution, les résidus ont augmenté jusqu’à atteindre un maximum vers la 6000ème itération, pour diminuer et enfin converger vers une valeur d’autant plus proche de zéro. Ici, il fallait choisir une tolérance suffisamment faible pour que l’algorithme ne s’arrête pas trop vite (on observe que les résidus restent tout de même relativement proche de 0) sur une solution améliorable. Aussi, le nombre d’itération devait être suffisamment élevé, pour la valeur du pas de 0.2 (nous ne voulions pas plus augmenter sa valeur pour minimiser le risque de divergence), de sorte que la descente de gradient atteigne le minimum après plus de 8000 itérations (et que la "bosse" à environ 6000 itértions soit dépassée).

Fitting du modèle

Sur le graphique ici présent, nous pouvons visualiser, avec les paramètres "a" et "b" (calculés lors de la régression logistique), la conformité du modèle logistique aux données du dataset. La courbe ne passe malheureusement pas par ces points. Mais cela ne signifie pas pour autant que le modèle est mauvais. En effet, on observe que pour des scores proches (voire égaux), les deux niveaux de concentration sont possibles, rendant la classification difficile. Ce d’autant plus qu’il ne s’agit que d’une visualisation. Voyons d’autres aspects pour évaluer la qualité du modèle.

Analyse de performance

Avant tout, il faut savoir qu’il existe différente métriques d’évaluation d’un modèle selon la tâche que l’on veut qu’il effectue. Dans ce cas (où l’enjeu est moindre), nous proposons d’évaluer sa précision. Autrement dit, on voudrait voir la qualité du modèle dans sa capacité à identifier le niveau concentré. S’il était parfait en précision, et qu’il indiquait qu’un score correspondait à une concentration élevée (focused), alors les chances qu’il se trompe seraient faibles; choses qui ne serait pas le cas s’il évaluait le niveau de concentration comme divided. En bref, quand on utilise une métrique de précision, on "tolère" que le modèle se trompe, mais pas lorsqu’il identifie un niveau "1" (focused). Par ailleurs, pour pouvoir classifier une donnée, il faut établir un seuil (cut-off) permettant de statuer sur l’appartenance à une classe ou l’autre en fonction de la probabilité évaluée par le modèle logistique. Au dessus du cut-off, la valeur renvoyée sera 1 (focused), en-dessous, la valeur sera 0 (divided). À présent, nous allons évaluer la performance globale du modèle, en visualisant sa courbe ROC(4) (à droite).

Pour ce faire, nous choisissons un certain nombre de seuils, auxquels on associera les matrices de confusions du modèle et représentons, par la suite, le point (taux de vrais positifs(5), taux de faux positifs(6)) sur un graphique jusqu’à construire la courbe ROC comme celle représentée à droite de ce paragraphe. D’ailleurs, dans ce dernier, on constate que l’on a une visualisation complète de la méthodologie. L’AUC(7) est d’environ 0.8, signe que le modèle n’est pas nécessairement mauvais mais peut ne pas être suffisamment satisfaisant. Aussi, on observe que le seuil optimal est de 0.32 mais encore faut-il préciser dans quel mesure ce seuil est optimal. Eh bien, il est optimal dans la mesure où il garantie la meilleure association entre un taux de vrais positifs le plus élevé possible tandis que le taux de faux positifs est le plus faible possible. Une façon d’évaluer cela est de regarder l’écart vertical des points à la droite "y=x": le point pour lequel cette distance est maximale correspondra au seuil optimal (ici 0.32). En résumé, à travers ces quelques paragraphes, nous avons tenté d’expliquer le principe de la régression logistique. Nous en avons nous-mêmes implémenté une en proposant un algorithme d’optimisation classique: la descente de gradient à pas fixe pour minimiser l’erreur quadratique moyenne. Enfin, le modèle ainsi conçu fut évaluer, en termes de performances, via la construction de sa courbe ROC.

Remarques : 1) Le modèle fut entraîné et évalué sur le même jeu de données ("attention" de seaborn) ; sa performance n’est donc évalué que sur des données qu’il a déjà "vu" (elle serait donc sans doute plus faible sur un nouveau jeu de données). 2) Les méthodes employées sont, sans doute, perfectibles et la façon d’employer la régression logistique, dans le cadre strict de ce jeu de données qui n’a pas subi de traitement particulier (si ce n’est l’encodage des modalités), l’est certainement tout autant. Cela dit, l’unique but du présent écrit est de présenter le principe de fonctionnement d’une régression logistique en abordant que partiellement les détails techniques, plusieurs ont été omis (notamment dans la partie sur l’optimisation où l’algorithme n’est que très peu expliquée)


  1. Il semblerait qu’en général, pour de la régression logistique binaire, on choisisse le logit comme métrique à optimiser car l’erreur quadratique moyenne présenterait plus d’extrema locaux, augmentant la difficulté dans la recherche de l’optimum.

  2. On peut choisir d’aller dans le sens du gradient, ou à l’opposé de ce dernier, selon que l’on veuille aller vers un minimum ou un maximum de la fonction à optimiser.

  3. Valeur en-dessous de laquelle on considère que l’on est suffisamment proche d’un extremum.

  4. ROC: Receiver Operating Characteristic. C’est une courbe, utilisée en biologie, qui représente le taux de vrais positifs en fonction du taux de faux positifs pour chaque valeur de seuils choisies. Idéalement, il faudrait que le taux de vrais positifs soit maximal (100%) tandis que le taux de faux positifs soit minimal (0%) pour chaque seuil. Une telle courbe permet deux choses : 1) voir la performance globale du modèle 2) choisir un seuil optimal.

  5. Le nombre de vrais positifs rapporté à tous les positifs (faux négatifs + vrais positifs).

  6. Le nombre de faux positifs rapporté à tous les négatifs (faux positifs + vrais négatifs).

  7. AUC : Area Under Curve. C’est l’aire sous la courbe ROC. Plus elle est proche de 1 et plus cela signifie que le modèle est bon car le taux de vrais positifs a tendance à être élevé quel que soit le seuil et le taux de faux positifs.